The individual exam consisted of 30 multiple choice questions. 5 points were awarded for each correct answer, 1 point for each unanswered question, and 0 points for each incorrect answer. No calculators allowed.
The thirty questions and their solutions
How many solutions are there for the equation \( \ \ x-1=\sqrt{2x+1} \ \) ?
- 0
- 1
- 2
- 3
- 4
Answer: (b)
Solution: The equation has only one solution, \( x=4 \) . One might get the extraneous solution \( x=0 \) by squaring the two sides of the equation.
What is the sum of all positive integer divisors of 2020?
- 505
- 2021
- 3360
- 4284
- 5025
Answer: (d)
Solution: The prime decomposition of 2020 is 22⋅ 5 ⋅ 101, so the sum of the positive divisors is (1+2+4)⋅(1+5)⋅(1+101) = 4284
An engineer can finish a highway section in 3 days with his present supply of a certain type of machine. However, with 3 more of these machines the job could be done in 2 days. If the machines all work at the same rate, how many days would it take to do the job with one machine?
- 6
- 12
- 15
- 18
- 36
Answer: (d)
Solution: If \( x \) is the number of machines that can finish the job in 3 days, then \( 3x=2(x+3) \) is the number of days that one machine would take to finish the job.
What is the largest possible area of a right triangle with hypotenuse of length 5 in?
- 5 in
- 5.5 in
- 5.725 in
- 6 in
- 6.25 in
Answer: (e)
Solution: Let \( x \) and \( y \) be the lengths of the legs of the right triangle. By the Pythagorean Theorem, \( x^2+y^2=25 \). The area of the triangle is \( A=\displaystyle\frac{xy}{2} \) , and by the inequality of geometrical and arithmetical means, \( A\leq\displaystyle\frac{x^2+y^2}{4}=\frac{25}{4} \) , with equality when \( x=y=5/\sqrt{2} \).
Let \( \alpha \) be an angle with \( \cos{\alpha}=\displaystyle\frac{1}{3} \) . Find the value of \( \displaystyle\sin{\alpha}\cdot\tan\frac{\alpha}{2} \) .
- \( –1/3 \)
- \( 1/3 \)
- \( \sqrt{3}/{3} \)
- \( 2/3 \)
- \( 1 \)
Answer: (d)
Solution: We use Double Angle Identities: \( \displaystyle\sin{\alpha}\cdot\tan\frac{\alpha}{2}=2\sin^2{\frac{\alpha}{2}}=1-\cos{\alpha}=\frac{2}{3} \) .
The polynomial \( f(x)=4x^3-2x^2+7x-9\) has two complex conjugate roots. What is the modulus (or absolute value) of such a complex root?
- 1/2
- 1
- 3/2
- 9/4
- 4
Answer: (c)
Solution: Observe that \( f(1)=0 \), so \( x=1 \) is the real root of \( f(x) \). Let the complex roots be \( a\pm bi \) . Then the product of the roots is \( 1\cdot(a+bi)\cdot(a-bi)=a^2+b^2 \) which is equal to \( \displaystyle\frac{9}{4} \) . Then the modulus is \( \sqrt{a^2+b^2}=\displaystyle\frac{3}{2} \) .
Five different colored pieces of candy are to be given to three children. How many ways can this be done so that each child gets at least one piece of candy?
- 125
- 150
- 175
- 225
- 250
Answer: (b)
Solution: The cases are one of the children gets 3 pieces while the other two get one and one
child gets 1 piece while each of the other two children get 2 pieces: \(
\displaystyle {3 \choose 1}{5\choose 3}{2\choose 1}+ {3 \choose 1}{5 \choose 1}{4
\choose 2} = 3\times10 \times 2 + 3 \times 5 \times 6 = 60 + 90 = 150 \) .
How many real roots does the equation \( \sin x= \log_{10} x \) have?
- 1
- 2
- 3
- 4
- more than 4
Answer: (c)
Solution: Since \( \sin x\leq 1 \) and when \( x>10 \) , \( \log_{10} x>1 \) , the solutions must be in (0,10). From the graphs of \( \sin x \) and \( \log_{10} x \) , we can find that there is one solution in (0, π), and two solutions in (2π, 3π) .
The two polynomials \( x^4 + 6x^2 + 25 \) and \( 3x^4 + 4x^2 + 28x + 5 \) have a common factor of the form \( x^2 + bx +c \) . What is \( b + c \) ?
- –2
- 0
- 1
- 2
- 3
Answer: (e)
Solution: Subtracting 3 times the first polynomial from the second and dividing the answer by –14 gives \( x^2 - 2x + 5 \) .
A square with each side of length 1 is inscribed in a circle. What is the length of a side of a square which is inscribed in one of the circular zones outside the given square? This square has two vertices on the side of the square with sides of length 1 and the other two vertices on the circle.

- \( 1/5 \)
- \( \sqrt{6}/10 \)
- \( 1/4 \)
- \( \sqrt{2}/5 \)
- \( \sqrt{2}/4 \)
Answer: (a)
Solution:
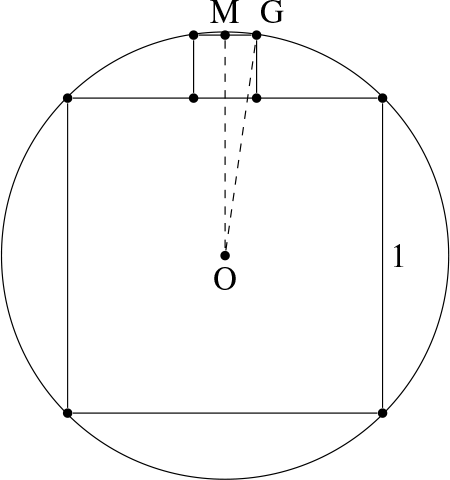
The radius of the circle is \( \displaystyle\frac{\sqrt{2}}{2} \) . Let \( x \) be the length of a side of the small square. Let \( O \) be the center of the circle and \( G \) be one of the vertices of the small square on the circle. If \( M \) is the midpoint of the side of the small square with endpoints on the circle, then the \( \triangle{OMG} \) is a right triangle with legs \( MG=\displaystyle\frac{x}{2} \), \( OM=x+\displaystyle\frac{1}{2} \), and hypotenuse \( OG=\displaystyle\frac{\sqrt{2}}{2} \). By the Pythagorean Theorem,
$$ \left(\frac{x}{2}\right)^2+\left(x+\frac{1}{2}\right)^2=\left(\frac{\sqrt{2}}{2}\right)^2 $$
Simplify and we get \( 5x^2+4x-1=0\), which has positive solution \( x=\displaystyle\frac{1}{5} \).
Bob plays the following game: He picks an integer n, and then 10 coins are flipped.
He wins if there are n heads or if there are n tails.
Which of the following choices for n gives Bob the maximal chance of winning?
- 1
- 2
- 3
- 4
- 5
Answer: (d)
Solution: In Pascal's Triangle, the largest numbers in each row are in the middle. If Bob picks n = 4, then his chance of winning cumulate the combinations \( \displaystyle {10 \choose 4}+ {10 \choose 6} \) , and this sum well exceeds \( \displaystyle {10 \choose 5} \) corresponding for the case when he picks n = 5.
If \( x=\dfrac{1}{\log_{\frac{1}{2}}\frac{1}{3}}
+\dfrac{1}{\log_{\frac{1}{5}}\frac{1}{3}} \) , then \(x\) is in the interval:
- (–1,0)
- (0,1)
- (1,2)
- (2,3)
- (3,4)
Answer: (d)
Solution: After simplification, \( x=\log_310 \).
Let \( f(x) \) be a function which is defined for all real numbers \( x \). Suppose that for every real number \( x \), we have \( f(x+3)f(x-3)=9 \). Also, for \( -3\leq x<3 \) , we have \( f(x)=|x| \). What is the value of \( f(2020) \) ?
- –2
- –3/2
- 2
- 9/2
- 2020
Answer: (d)
Solution: The function \( f(x) \) is periodic with period 12 as \( f(x)=\displaystyle\frac{9}{f(x+6)}=f(x+12) \) . Then, \( f(2020)=f(4)=\displaystyle\frac{9}{f(-2)}=\frac{9}{2} \) .
Sort the integers 1 through 6 randomly, and denote them as a, b, c, d, e, and f. What is the probability that abc+def is an even number?
- 1/10
- 1/2
- 9/10
- 19/20
- 1
Answer: (c)
Solution: The total number of choices is 6! = 720. Consider the cases when
abc+def is odd. Then, either abc or def has to be odd. The case abc is odd has (3!)×(3!)=36 choices. The same is true for the case def is odd. Therefore, the total number of choices with abc + def even is 720 – 36×2 = 648. The probability is \( \displaystyle\frac{648}{720}=\frac{9}{10} \) .
In triangle \( \triangle ABC \), line segment \( \overline{AM} \) bisects angle \( \angle{BAC} \) . The point \( M \) lies on side \( \overline{BC} \) . Let \( K \) be a point on \( \overline{AM} \) . The line \( \overleftrightarrow{BK} \) intersects side \( \overline{AC} \) at the point \( N \) , and line \( \overleftrightarrow{CK} \) intersects side \( \overline{AB} \) at the point \( P\) . Find the length of \( \overline{AP} \) if \( CN=1,\ AN=2 \) , and \( BP=3 \) .
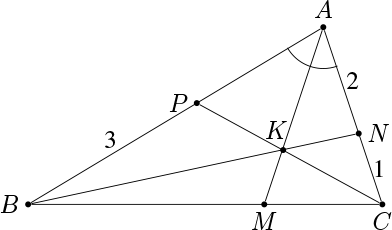
- 1.5
- 2.25
- 2.5
- 3
- 4
Answer: (d)
Solution: Let \( AP=x \) . By the Bisector Theorem, \( \displaystyle\frac{BM}{MC}=\frac{AB}{AC}=\frac{x+3}{3} \) . By Ceva's Theorem, \( \displaystyle\frac{AP}{PB}\cdot\frac{BM}{MC}\cdot\frac{CN}{NA}=1 \) , which, combined with the above, yields \( \displaystyle\frac{x}{3}\cdot\frac{x+3}{3}\cdot\frac{1}{2}=1 \) . This is equivalent with \( x^2+3x=18 \) , whose positive solution is \( x=3 \) .
If \( a>0 \) , \( a \neq 1 \) and \( F(x) \) is an odd function, then \( \displaystyle G(x)=F(x)\cdot\log_a\big(\sqrt{x^2+1}+x\big) \) is:
- odd
- even
- neither odd nor even
- symmetry depends on a
- no conclusion
Answer: (b)
Solution: Since \( \displaystyle \log_a\big(\sqrt{(-x)^2+1}-x\big)=\log_a\bigg(\frac{x^2+1-x^2}{\sqrt{x^2+1}+x}\bigg) =-\log_a\big(\sqrt{x^2+1}+x\big) \) is odd, and \( F(x) \) is an odd function, we have \( G(-x)=G(x) \) .
What is the minimum value of the function \( \displaystyle f(x)=\frac{5\
-4x+x^2}{2-x} \) on \( (-\infty,2) \) ?
- –1
- 0
- 1
- 2
- 3
Answer: (d)
Solution: If \( y=2-x> 0\) , then \( f(x)=y+\displaystyle\frac{1}{y}\geq 2 \) , by the arithmetic mean-geometric mean inequality. Since \( f(1)=2 \) , the minimum value of \( f(x) \) is 2.
How many tuples of positive integers \( (x,y,z,w) \) solve the equation
\( 8x^4+4y^4+2z^4=w^4 \) ?
- 0
- 1
- 2
- 4
- 8
Answer: (a)
Solution: Assume a solution exists. Let \( k \) be the smallest natural number such that a solution has \( w=2^k\cdot n \) , with \( n \) an odd positive integer. Then, by successively dividing by 2, \( z \) , \( y \) , and \( x \) must be even. Dividing again by 2, it follows that there is also a solution with \( w=2^{(k-1)}\cdot n \) . This contradicts the definition of \( k \).
Let \( x \) and \( y \) be real numbers. What is the minimum value of the following
function
$$ f(x,y)=\sqrt{x^2+1}+\sqrt{(y-1)^2+(3-x)^2}+\sqrt{(y-3)^2+1} \quad ? $$
- 0
- 2.5
- 5
- 10
- 25
Answer: (c)
Solution:
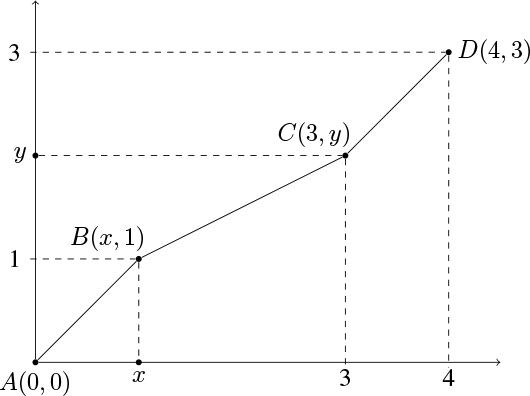
Let \( A(0,0) \) , \( B(x,1) \) , \( C(3,y) \) , and \( D(4,3) \) be points in the plane. Then the function \( f(x,y) \) is the sum of the distances \( AB + BC + CD \) , which is minimum if \( A \) , \( B \) , \( C \) , and \( D \) are collinear points in this order, which can be realized when \( x=4/3 \) and \( y=9/4 \) .
The minimum of \( f(x,y) \) is then the distance \( AD = 5 \) .
Let \( x \) be the real number satisfying the equation \( 2^x + 4^x + 8^x = 175 \) . Which of the following is closest to \( x \) ?
- 1.7
- 2
- 2.4
- 2.9
- ln(175)
Answer: (c)
Solution: The function \( f(y)=y+ y^2+ y^3 \) is an increasing function for \( y>0 \) . We make the estimates \( f(2^{9/4})=f(4\sqrt{\sqrt{2}})< f(4\sqrt{1.42})< f(4\cdot1.2)<f(5)=5+25+125<175 \) , and \( f(2^{5/2})=f(4\sqrt{2})=4\sqrt{2}+(4\sqrt{2})^2+(4\sqrt{2})^3=132\sqrt{2}+32>175 \) . Since \( y=2^x \) is also an increasing function of \( x \) , we have \( 2.25<x<2.5\) .
Let \( f_1(x)=\displaystyle\frac{2x-1}{1+x} \) and successively define \( f_{n+1}(x)=f_1(f_n(x)) \) for each positive integer \( n \) . Find \( f_{2020}(x) \) .
- \( x \)
- \( \displaystyle\frac{1}{1-x} \)
- \( \displaystyle\frac{x-1}{x} \)
- \( \displaystyle\frac{1}{x} \)
- \( \displaystyle\frac{x+1}{2-x} \)
Answer: (b)
Solution: Observe that \( f_1(x)=\displaystyle 2-\frac{3}{1+x} \) , \( f_2(x)=\displaystyle2-\frac{3}{1+2-\frac{3}{1+x}}=2-\frac{1+x}{x}=1-\frac{1}{x} \) , \( f_4(x)=\displaystyle1-\frac{1}{1-\frac{1}{x}}=\frac{1}{1-x} \) , \( f_6(x)=f_2(f_4(x))=\displaystyle1-\frac{1}{\frac{1}{1-x}}=x \) , so \( f_{6k}(x)=x \) for every positive integer \( k \) . Then \( f_{2020}(x)=f_{6\cdot 336+4}(x)=f_4(x)=\displaystyle\frac{1}{1-x} \) .
What is the expected number of times a person must toss a fair coin to get 3 consecutive heads?
- 6
- 8
- 10
- 12
- 14
Answer: (e)
Solution: Let \( x \) be the number of coin flips to get 3 consecutive heads. Either the coin flip starts with a tail with probability \( P(T...)=1/2 \) and we have wasted a toss, so we will have to flip the coin \( x+1 \) number of times, a head followed by a tail with a probability \( P(HT..)=1/4 \) and we will have to flip the coin \( x+2 \) times, two heads followed by a tail with probability \( P(HHT..)=1/8 \) and we will have to flip the coin \( x+3 \) times, or three heads with probability \( P(HHH)=1/8 \) in which case we have flipped the coin 3 times. Then
$$ x=P(T...)(x+1)+P(HT...)(x+2)+P(HHT...)(x+3)+P(HHH)\cdot 3, $$
$$ \text{so}\ \ x=\frac{1}{2}(x+1)+\frac{1}{4}(x+2)+\frac{1}{8}(x+3)+\frac{1}{8}\cdot 3,\text{ which gives }x=14. $$
What are the endpoints, in real numbers, of the following interval?
$$ \displaystyle
\left[\cos\frac{\pi}{9}+\cos\frac{7\pi}9+\cos\frac{5\pi}9,\ \ \
\cos\frac\pi9\cos\frac{7\pi}9\cos\frac{5\pi}9\right] $$
- 0 and 1/8
- –1/9 and 1/2
- –1/9 and 1/8
- 0 and 1/2
- none of these
Answer: (a)
Solution: The answer follows from
$$\displaystyle\cos\frac\pi9+\cos\frac{5\pi}9+\cos\frac{7\pi}9= 2\cos\frac\pi3\cos\frac{2\pi}9-\cos\frac{2\pi}{9}=0, $$
$$\text{ and } \displaystyle\cos\frac\pi9\cos\frac{7\pi}9\cos\frac{5\pi}9= \frac12\left(\cos\frac{8\pi}9+\cos\frac{2\pi}3\right)\cos\frac{5\pi}9=\frac12\left(-\cos\frac{\pi}9-\frac12\right)\left(-\cos\frac{4\pi}9\right) $$
$$ =\frac14\left(\cos\frac{5\pi}9+\cos\frac\pi3\right)+\frac14\cos\frac{4\pi}9=\frac18. $$
Jack, Ken and Lee walk clockwise around a circular track. It takes Jack, Ken, and Lee respectively 6, 10, and 14 minutes to finish each lap. They start at the same time and at the same point on the track. How many minutes into the walk will they all be at the same spot on the track again?
- 20
- 40
- 105
- 210
- 840
Answer: (c)
Solution: Let \( s \) be the number of minutes after which Jack catches up with Ken, going one more lap then Ken, and \( t \) be the number of minutes after which Ken catches up with Lee, going one more lap. These hold:
\( \displaystyle\frac{1}{10}s+1=\frac{1}{6}s,\text{with solution } s=15 \) minutes and
\( \displaystyle\frac{1}{14}t+1=\frac{1}{10}t \) , with solution \( t=35 \) minutes.
All three will be at the same spot into the walk after a common multiple of \(s\) and \(t\). The least common multiple is 105 minutes.
What is the largest number of non-overlapping circles of radius \( \displaystyle\frac{1}{3} \) that can be placed around a circle of radius 1 so that all the ones of radius \( \displaystyle\frac{1}{3} \) touch the one of radius 1, without necessarily touching each other?
- 12
- 13
- 15
- 17
- 18
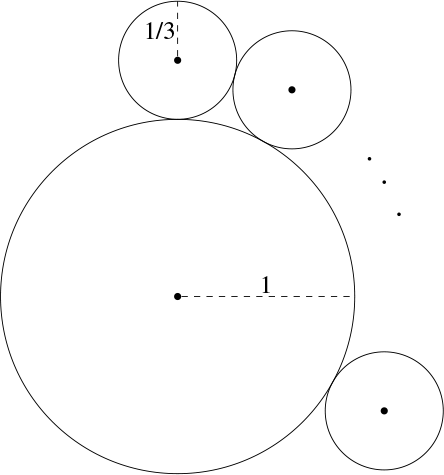
Answer: (a)
Solution:
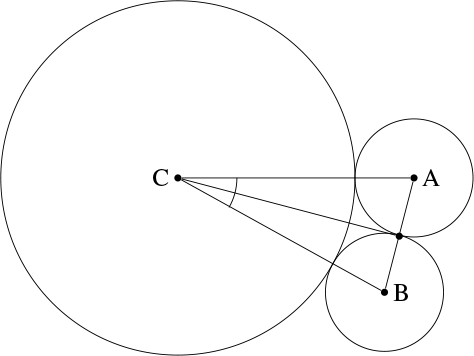
Let C be the center of the circle of radius 1 and A and B the centers of two consecutive circles of radius 1/3. The shortest possible distance AB is when these circles are tangent, where AB = 2/3. If the number of small circles is n, then \( \angle{ACB}=\alpha\leq 2\pi/n \). We have \( \alpha/2>\sin(\alpha/2)=1/4 \) , so, \( \pi/n>1/4 \). The largest integer such that \( n<4\pi \) is \( n=12 \) , which is the only possible answer.
Note that, in radians, \( \sin(\alpha/2)=1/4 \) implies \( \alpha=0.505.. \) which makes \( 2\pi/\alpha=12.432... \) so \( n=12 \) is possible.
In the Cartesian system of coordinates, let the set \( K=\{(x,y)~|~x \text{ and } y \text{ are in }\{-1,0,1\}\} \) . Choose 3 points in the set \( K \) randomly. What is the probability that at least one of the distances between 2 of the 3 points is exactly \( \sqrt{5} \) ?
- 2/7
- 1/3
- 4/7
- 13/21
- 2/3
Answer: (c)
Solution:
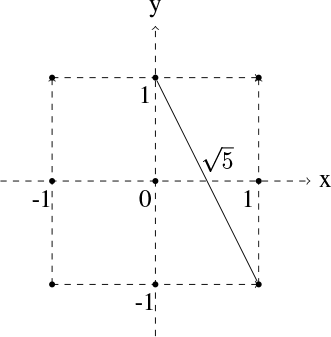
The total number of ways of choosing 3 points out of 9 points is \( \displaystyle{9\choose3}=84 \) . There are 8 different pairs of points with the distance between them equal to \( \sqrt{5} \) . The third point can be chosen from the remaining 7 points, which leads to a total number of \( 8\times7=56 \) choices. We need to exclude the cases that have been double-counted, where the 3 points have two pairs of points with distances \( \sqrt{5} \) . There are a total of 8 such cases. Finally, the number of choices of 3 elements in $K$ such that the distance between 2 of them is \( \sqrt{5} \) is \( 56-8=48 \) , and therefore, the probability is \( \displaystyle\frac{48}{84}=\frac{4}{7} \) .
Which one of the following is a correct conclusion about the equation
$$ \displaystyle \arccos\bigg(\frac45\bigg)-\arccos\bigg(-\frac45\bigg)=\arcsin (x)\ \ ? $$
- \( x=-24/25 \)
- \( x=0 \)
- \( x=16/25 \)
- \( x=24/25 \)
- There is no solution for \( x \)
Answer: (e)
Solution: From the condition, we know that \( \displaystyle \arcsin (x)=2\arccos\bigg(\frac45\bigg)-\pi \) . Let \( \theta=\displaystyle \arccos\bigg(\frac45\bigg) \) . Then \( \displaystyle \cos\theta=\frac45 \) and \( \displaystyle \sin\theta=\frac35 \) . So \( \displaystyle \cos\theta>\sin\theta>0 \) , which implies \( 0< \theta <\displaystyle\frac{\pi}{4} \) . Thus, \( \displaystyle 2\theta<\frac{\pi}2 \) . Then \( \arcsin{x}=\displaystyle 2\theta-\pi< -\frac{\pi}2 \) , which is wrong. Therefore, there is no solution for \( x \) .
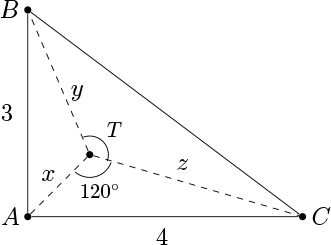
The Torricelli point \( T \) of the right triangle \( \triangle{ABC} \) with legs \( AB=3 \) and \( AC=4 \) is such that \( \angle{ATB}=\angle{ATC}=\angle{BTC}=120^\circ \) . If \( AT=x \) , \( BT=y \) , and \( CT=z \) , then what is the value of the expression \( xy+yz+zx \) ?
- \( 4\sqrt{3} \)
- \( 6\sqrt{2} \)
- \( 4\sqrt{6} \)
- \( 8\sqrt{2} \)
- \( 8\sqrt{3} \)
Answer: (e)
Solution: We have, on one hand, that the area of triangle \( ABC \) is
$$ \begin{align*} S_{ABC}&=S_{ATB}+S_{BTC}+S_{CTA} \\
&=\frac{1}{2}\left(xy\sin{120^o}+yz\sin{120^o}+zx\sin{120^o}\right) \\
&=\frac{\sqrt{3}}{4}\left(xy+yz+zx\right). \\
\end{align*} $$
On the other hand, triangle \( ABC \) is a right triangle with legs \( \overline{AB} \) and \( \overline{AC} \) , so
\( \displaystyle S_{ABC}=\frac{3\cdot 4}{2}=6. \quad \text{Thus, }xy+yz+zx= 6\cdot\frac{4}{\sqrt{3}}=8\sqrt{3}.\)
If \( \displaystyle f(x)=\frac{4^x}{4^x+2} \) , then
$$\displaystyle f(0)+ f\bigg(\frac{1}{2020}\bigg)+f\bigg(\frac{2}{2020}\bigg)+f\bigg(\frac{3}{2020}\bigg)
+ \cdots + f\bigg(\frac{2019}{2020}\bigg) + f(1) \quad \text{ is } $$
- 1001
- 2019/2
- 1010
- 2021/2
- 2020
Answer: (d)
Solution: Observe that \( \displaystyle f(x)=\frac{2^x}{2^x+2^{1-x}} \) . Then \( f(x)+f(1-x)=1 \) . Hence the sum is equal with half the number of its terms. The inputs have numerators the integers from 0 to 2020, so the sum is 2021/2.
Let \( A, B, C, D, E, F, G, \) and \( H \) be the vertices of a cube as shown. Let \( K \) be a point on the edge \( \overline{EF} \) . Suppose that the plane that goes through \( A, C, \) and \( K\) divides the cube into two parts with the ratio of their volumes 2:1 and with the smaller part containing the points \(B\) and \(F\). What is the value of \( \displaystyle\frac{KF}{EK} \) ?
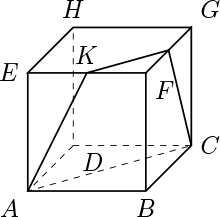
- \( \displaystyle\frac{\sqrt{3}}{3} \)
- \( \displaystyle\frac{\sqrt{5}-1}{2} \)
- 1
- \( \displaystyle\frac{\sqrt{5}+1}{2} \)
- \( \sqrt{3} \)
Answer: (d)
Solution:
Without loss of generality, we set the side length of the cube to be 1, and \( KF=x \) . Extend \( \overline{AK} \) and \( \overline{BF} \) and denote their intersection by \( P \). Let \( PF=y \) . By the similarity of the triangles \( \triangle{PKF} \) and \( \triangle{PAB} \) , we get \( \displaystyle\frac{x}{1}=\frac{y}{y+1} \) . Therefore, \( y=\displaystyle\frac{x}{1-x}=\frac{KF}{EK} \) . By the assumption, the volume of the solid with vertices \( A, B, C, K, F, \) and \( L \) is \( \displaystyle\frac{1}{3} \) . Also, it is the difference of the volumes of the right tetrahedrons with vertices \( P,A, B \), and \( C \) and with vertices \( P, K, F \), and \( L \). Hence,
$$ \frac{y+1}{6}-\frac{x^2y}{6}=\frac{1}{3}\quad\Rightarrow\quad
y+1-\frac{y^3}{(y+1)^2}=2\quad\Rightarrow\quad
y^2-y-1=0\quad\Rightarrow\quad y=\frac{1+\sqrt{5}}{2}. $$
The team round consists of 10 questions with short response answers (e.g., answers will consist of one or more numbers, a polynomial, etc.) and one or more open-ended questions.
Each student received a copy of the questions, and the team recorded their answers on an answer sheet. Teams scored 10 points for each question answered correctly.
Acknowledgment: Some questions were taken or adapted from Challenging Problems in Algebra and Challenging Problems in Geometry by Alfred Posamentier and Charles Salkind.
What is the maximum value of \( (\sin x - \cos x)^2 \) ?
Answer: 2
Multiply it out to get
$$ \begin{align*}
(\sin x - \cos x)^2 & = \sin^2(x) - 2 \sin(x) \cos(x) + \cos^2(x) \\
& = 1 - 2 \sin(x) \cos(x) \\
& = 1 - \sin(2x). \\
\end{align*} $$
This is maximized when \( \sin(2x) = -1 \) , for example when \( x = - \pi/4 \). So the maximum value is \( 2 \) .
You flip six coins. What is the probability that the number of heads is divisible by \( 3 \)?
Answer: \( \frac{11}{32} \)
There are \( 2^6 = 64 \) total possibilities for the sequence of coin flips. There
is exactly one way to get all heads and one way to get all tails. The number of ways
to get three heads is
\[
{6 \choose 3} = 20,
\]
and so the answer is
\[
\frac{1 + 20 + 1}{64} = \frac{22}{64} = \frac{11}{32}.
\]
Beginning with a circle \( C_1 \) of radius \( 1 \), you inscribe an equilateral triangle \( T_1 \) in \( C_1 \). You then inscribe a circle \( C_2 \) inside \( T_1 \), an equilateral triangle \( T_2 \) inside \( C_2 \), a circle \( C_3 \) inside \( T_2 \), and so on indefinitely.
What is the radius of \( C_{10} \)?
Answer: \( \frac{1}{512} \) or \( \frac{1}{2^9} \) or \( 2^{-9} \).
The following picture shows \( C_1 \), \( T_1 \), and \( C_2 \) :
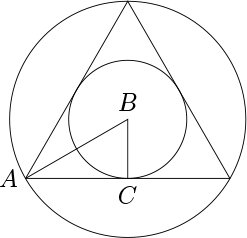
Since \( \overline{BA} \) lies on an angle bisector of the largest triangle, we see that \( \triangle BAC \) is a \( 30-60-90 \) triangle. Therefore \( BC = \frac{1}{2} AB = \frac{1}{2} \).
By the same reasoning, each circle \( C_{i + 1} \) has half the radius of the previous one \( C_i \). Since it is nine steps from \( C_1 \) to \( C_{10} \), the tenth circle has radius \( 2^{-9} \).
A bug starts at node D in the graph below. At each step, it randomly chooses an edge adjacent to its current node, and walks to the node on the other end of this edge. It repeats this process until it arrives at either node F or node C. (Backtracking is permitted.)
What is the probability it ends up at node F?
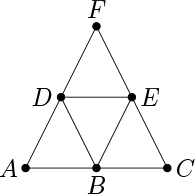
Answer: \( \frac{3}{5} \)
For each node \( X \), let \( p(X) \) be the probability of ending up at node \( F \), if the bug starts at \( X \) .
Then \( p(F) = 1 \) and \( p(C) = 0 \) . We also have \( p(A) = p(E) = \frac{1}{2} \)
by the symmetry of the diagram.
Also by symmetry, we have \( p(B) = 1 - p(D) \) .
Finally, we have
$$ \begin{align*} p(D) &= \frac{1}{4} \left( p(F) + p(E) + p(B) + p(A) \right) \\
&= \frac{1}{4} \left(1 + \frac12 + 1 - p(D) + \frac12\right) \\
&= \frac{3}{4} - \frac{p(D)}{4}. \\
\end{align*} $$
Solving, we get \( p(D) = \frac{3}{4} \cdot \frac{4}{5} = \frac{3}{5} \) .
In the United States, Chicken McNuggets are sold in boxes of 4, 6, 10, 20, or 50. (The former 9-piece box has been discontinued.)
If you buy exactly three boxes of Chicken McNuggets, how many different quantities of McNuggets can you obtain?
Answer: 32
There are \( {7 \choose 4} = 35 \) ways to choose three box sizes, allowing repetition. We have
$$ \begin{align*}
4 + 4 + 10 & = 6 + 6 + 6, \\
4 + 6 + 20 & = 10 + 10 + 10, \\
4 + 6 + 50 & = 20 + 20 + 20, \\
\end{align*} $$
and it can be checked that these are the only choices yielding the same number of McNuggets. (For example, look at the number of McNuggets \( \pmod{10} \) — this verification becomes much easier!) So the answer is \( 35 - 3 = 32 \) .
Let \( x \) and \( y \) be the smallest positive integers such that \( 9x - 11y = 1 \) and \( x + y > 2020 \). Find \( x - y \).
Answer: 203
The first step is to find integers \( x \) and \( y \) satisfying \( 9x - 11y = 1 \). Although there are shortcuts, trial and error works well also: \( x = 5 \) and \( y = 4 \) is a solution.
Now, if \( (5, 4) \) is a solution, so is \( (5 + 11n, 4 + 9n) \), for any positive integer \( n \). Moreover, you can convince yourself that these are the only solutions, although it takes a bit of work to prove.
We want
\[
(5 + 11n) + (4 + 9n) > 2020,
\]
or \( 9 + 20n > 2020 \). The smallest solution to this inequality is \( 101 \). So
our pair \( (x, y) \) is given by
\[
(5 + 11 \cdot 101, 4 + 9 \cdot 101),
\]
and the answer to our question is
\[
(5 + 11 \cdot 101) - (4 + 9 \cdot 101) = 1 + 2 \cdot 101 = 203.
\]
How many real solutions are there to the system of equations
\[
x^2 + y^2 = 4, \ \ y = x - x^3?
\]
Answer: 2
Trying to solve this algebraically is messy. The best solution is to draw a careful graph (not reproduced here).
In the picture below, \( \overline{AB} \perp \overline{BC} \), \( \overline{DC} \perp \overline{BC} \), and \( \overline{PQ} \) is the perpendicular bisector of \( \overline{AD} \).
If \( AB = 9 \), \( BC = 8 \), and \( DC = 7 \), find the area of the quadrilateral \( APQB \).
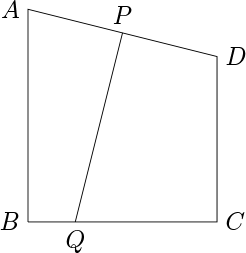
Answer: 26
Let \( R \) lie on \( \overline{BC} \) so that \( \overline{BC} \perp \overline{PR} \). Then, since \( P \) is the midpoint of \( AD \), \( PR = 8 \).
Moreover, the slope of \( \overline{QP} \) is \( 4 \), since that of \( \overline{AD} \) is \( - \frac{1}{4} \). This implies that \( QR = 2 \).
The area of quadrilateral \( APRB \) is \( \frac{9 + 8}{2} \cdot 4 = 34 \), and that of triangle \( PQR \) is \( \frac{1}{2} \cdot 2 \cdot 8 = 8 \).
So the answer is \( 34 - 8 = 26 \).
Find the sum of those positive integers \( n \leq 2020 \) for which \( \sqrt{n - 8} + \sqrt{n + 8} \) is an integer.
Answer: 25
We have
\[
\left( \sqrt{n - 8} + \sqrt{n + 8} \right)^2 = 2n + \sqrt{n^2 - 64} \quad ,
\]
which must be the square of an integer.
In particular, \( n^2 - 64 \) must be the square of an integer. If \( n^2 - 64 = m^2 \), then \( n \) and \( m \) must be of the same parity, and the largest possible \( n \) is equal to \( 17 \), because \( n^2 - 64 > (n - 2)^2 \) whenever \( n > 17 \).
We check that the only \( n \leq 17 \) for which \( n^2 - 64 \) is an integer square are \( n = 8, 10, 17 \). Of these, only \( n = 8 \) and \( n = 17 \) yield an integer solution to our original equation.
There is exactly one integer \( < 1500 \) which can be written as the sum of two positive integer squares in at least four ways. What is it? (Count \( n = a^2 + b^2 \) and \( n = b^2 + a^2 \) as being the same.)
Hint: if \( m \) and \( n \) can be written as the sum of integer squares, then so can
\( mn \):
\[
(a^2 + b^2)(c^2 + d^2) = (ac - bd)^2 + (ad + bc)^2.
\]
Answer: 1105.
\[
1105 = 4^2 + 33^2 = 9^2 + 32^2 = 12^2 + 31^2 = 23^2 + 24^2.
\]
The key is to notice that
$$\begin{align*}
(a^2 + b^2)(c^2 + d^2) & = (ac - bd)^2 + (ad + bc)^2, \\
(b^2 + a^2)(c^2 + d^2) & = (bc - ad)^2 + (bd + ac)^2,
\end{align*} $$
and the expressions on the right are (usually) different ways of writing \( (a^2 + b^2)(c^2 + d^2) \) as a product of two squares. So, it's a good idea to try multiplying together smaller numbers which are themselves products of two squares. \( 5 \), \( 13 \), and \( 17 \) all fit the bill, and \( 1105 = 5 \cdot 13 \cdot 17 \), and each of \( 5 \), \( 13 \), and \( 17 \) can be written as the sum of two squares, we can see that \( 1105 \) is an excellent integer to check. A bit of computation verifies that it does indeed work.
Proving that this is the unique solution, without brute force, requires much more effort.
Elimination Round
The top 16 scorers from the individual test were pitted against each other for an elimination round. For each question, participants had 90 seconds to come up with the correct answer. The first two participants to correctly answer three questions moved on to the head-to-head final round.
Three of the contestants each got their third correct answer on question four. The tie-breaker question, which also had a 90-second time limit, was posed to thos three contestants. The answer is a positive integer, and discovering the answer exactly in 90 seconds is probably impossible. The two answers closest to the correct answer (in either direction) determined who went to the final round.
Solve for \(x\) :
\[
|2x - 1| = |2x - 2|
\]
Answer: \( \frac{3}{4} \)
We have
\[
2x - 1 = \pm (2x - 2),
\]
and since \(+\) is impossible, we have
\[
2x - 1 = - (2x - 2) = -2x + 2.
\]
So,
\[
4x = 2 + 1 = 3 \Longrightarrow x = \frac{3}{4}.
\]
In the diagram below, three circles of equal size are inscribed in an equilateral triangle, so that they are tangent to each other and to the indicated sides of the triangle.
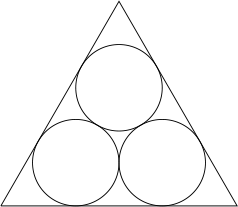
If each circle has radius 1, what is the side length of the triangle?
Answer: \( 2 + 2\sqrt{3} \)
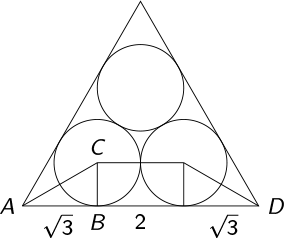
As \( \overline{AC} \) lies on an altitude, we have\( \angle CAB = 30 {}^\circ \) .
Hence \( AB = \sqrt{3} \) and so \( AD = 2 + 2 \sqrt{3} \) .
What is the only real solution \( x \) to
\[
\frac{x + 5}{x + 4} - \frac{x + 6}{x + 5} = \frac{x + 7}{x + 6} - \frac{x + 8}{x +
7} \quad ?
\]
Answer: \( - \frac{11}{2} \)
\[
\frac{(x + 5)^2 - (x + 4)(x + 6)}{(x + 4)(x + 5)} = \frac{(x + 7)^2 - (x + 6)(x +
8)}{(x + 6)(x + 7)}
\]
\[
\frac{1}{(x + 4)(x + 5)} = \frac{1}{(x + 6)(x + 7)}
\]
\[
(x + 4)(x + 5) = (x + 6)(x + 7)
\]
You can solve this for \(x\), or notice that \( - \frac{11}{2} \)lies on the midpoint
of symmetry of the roots.
\[
123 \times 321 = 41703
\]
In what number base is this equation true?
Answer: 8
\[
(b^2 + 2b + 3) \times (3b^2 + 2b + 1) = \cdots + 8b + 3.
\]
So \( b \mid 8 \) . Since the digit \( 7 \) appears in the product, \( b = 8 \) .
How many integers \( n \leq 2020 \) can be written in the form
\[
n = a^3 + b^3 + c^3,
\]
where \( a, b, c \) are positive integers?
Answer: 245
We must have \( 1 \leq a, b, c \leq 12 \) . Start with the number of such triples ( \( 12^3 = 1728 \) ).
Divide by \( 6 \) to get \( 288 \) , because most triples are counted six times:
\[ {\tiny
a^3 + b^3 + c^3 = a^3 + c^3 + b^3 = b^3 + a^3 + c^3 = b^3 + c^3 + a^3 = c^3 + a^3
+ b^3 = c^3 + b^3 + a^3 }
\]
Add a little bit, because triples with \(a = b\) , \( a = c \) , or \( b = c \) were
counted fewer than six times.
Subtract a little bit, e.g. for
\[
1730 = 10^3 + 9^3 + 1^3 = 12^3 + 1^3 + 1^3,
\]
Subtract a little bit, because \(a\), \(b\), and \(c\) can't all be close to \(12\).
To get the exact answer, ask a computer.
Final Round
The two finalists competed head-to-head to be the first to answer three questions correctly. To answer, contestants could buzz in any time (even before the question had been fully read aloud). A wrong answer reset the clock to 90 seconds for the other contestant to answer.
In 2019, Andrew Booker found the first known integer solution to \( a^3 + b^3 + c^3 = 33 \) .
One digit in his solution has been replaced by a question mark. What is the missing digit?
$$ \begin{align*}
33 & = 8866128975287528^3 \\
& + (-877840544286223?)^3 \\
& + (-2736111468807040)^3.
\end{align*} $$
Answer: 9
Modulo 10, we have
\[
3 \equiv 8^3 + (-?)^3 + 0^3 \equiv 512 + (-?)^3,
\]
so
\[
1 \equiv (-?)^3,
\]
for which \( -? \equiv 1 \) is the unique solution. So \( ? = 9 \) .
Solve for \( x \) :
\[
\log_3(9x) + \log_9(3x) = 7
\]
}
Answer: 27
Rewrite the equation as
\[
\log_3(9) + \log_3(x) + \log_9(3) + \frac{1}{2}\log_3(x) = 7,
\]
or
\[
\frac{5}{2} + \frac{3}{2} \log_3(x) = 7.
\]
So
\[
\frac{3}{2} \log_3(x) = 7 - \frac{5}{2} = \frac{9}{2},
\]
and \( \log_3(x) = 3 \) , so \( x = 27 \) .
What is the smallest value of \( r \) for which the following is true?
The parabola ( y = x^2 \) intersects (in at least one point) the circle with center \( (0, 1) \)and radius $r$ .
Answer: \( \frac{ \sqrt{3}}{2} \) .
Solving \( y = x^2 \) and \( x^2 + (y - 1)^2 = r^2 \) yields
\[
y^2 - y + (1 - r^2) = 0,
\]
\[
y = \frac{1 \pm \sqrt{1 - 4(1 - r^2)}}{2},
\]
\[
y = \frac{1 \pm \sqrt{-3 + 4r^2}}{2}.
\]
This has a nonnegative solution when \( -3 + 4r^2 \geq 0 \) , so when \( r^2 \geq
\frac{3}{4} \) .
Your friend rolls two ordinary dice and you roll one.
What is the probability that your die roll exceeds the total of hers?
Answer: \( \frac{5}{54} \)
Depending on whether you roll 1, 2, 3, 4, 5, or 6, the probability that her total
is lower is respectively
\[
0, 0, \frac{1}{36}, \frac{3}{36}, \frac{6}{36}, \frac{10}{36}.
\]
So the overall probability is
\[
\frac{1}{6} \left( \frac{1}{36} + \frac{3}{36} + \frac{6}{36} + \frac{10}{36} \right)
= \frac{1}{6} \cdot \frac{20}{36} = \frac{20}{216} = \frac{5}{54} \quad .
\]